Lineas paralelas
Paralelas cortadas por una transversal
Si dos rectas paralelas son cortadas por una transversal, entonces formaran ángulos
correspondientes congruentes.
Ángulos entre dos rectas paralelas cortadas por una transversal
Ángulos correspondientes
Son los que están al mismo lado de las paralelas y al mismo lado de la transversal son los ángulos que se ubican en las esquinas correspondientes y valen lo mismo.
Ángulos alternos externos
Son los que "fuera" de las paralelas a distinto lado de ellas y a distinto lado de la transversal. Son iguales entre sí; es decir miden lo mismo.
Ángulos alternos internos
Son los que están entre las paralelas a distinto lado de ellas y a distinto lado de la transversal. Son iguales entre sí; es decir miden lo mismo.
El quinto postulado de Euclides
si una recta al incidir sobre dos rectas hace los ángulos internos del mismo lado menores que dos rectos, las dos rectas prolongadas indefinidamente se encontrarán en el lado en el que están los ángulos menores que dos rectos.
1. La suma de las medidas de los ángulos de cualquier triángulo es igual a la suma de las medidas de dos ángulos rectos.
2. Las rectas paralelas están a la misma distancia de un mismo punto
3. Por un punto exterior a una recta dada sólo cabe trazar una paralela. Esta formulación es la más conocida y es debida al matemático griego Proclo.
4. Dos rectas paralelas guardan entre sí una distancia finita.
5. Las rectas no equidistantes convergen en una dirección y divergen en la opuesta.
6. Todos los puntos equidistantes de una línea recta, situados a un lado determinado de ella, constituyen una línea recta.
7. Sobre una recta finita siempre se puede construir un triángulo semejante a un triángulo dado.
8. Existe un par de triángulos no congruentes, pero semejantes.
9. En todo cuadrilátero que contenga tres ángulos rectos, el cuarto ángulo también es recto.
10. Se puede construir un triángulo cuya área sea mayor que cualquier área dada.
11. Dados tres puntos no alineados, siempre será posible construir un círculo que pase por todos ellos.
12. No hay patrón métrico absoluto de longitud.
Euclides presenta el anunciado como un axioma: su quinto postulado.
1. Postúlese el trazar una línea recta desde un punto cualquiera hasta un punto cualquiera.
2. Y el prolongar continuamente una recta finita en línea recta.
3. Y el describir un círculo con cualquier centro y distancia.
4. Y el ser todos los ángulos rectos iguales entre sí.
5. Y que si una recta al incidir sobre dos rectas hace los ángulos internos del mismo lado menores que dos rectos, las dos rectas prolongadas indefinidamente se encontrarán en el lado en el que están los menores que dos rectos.
Aplicaciones de la geometría en la ciencia y el arte
La geometría puede aplicarse para muchas cosas como: hacer planos para casas, hacer imágenes en una computadora o a mano, e incluso para imprimir con una impresora 3D. Aquí nos centraremos en las aplicaciones que tiene en la ciencia y el arte con algunas imágenes. Donde ejemplificamos los videojuegos (que están hechos a base de figuras geométricas), un tipo de arte que es el cubismo (donde observamos que los autores usan solo figuras geométricas para crear la pintura) y la reciente impresora que puede imprimir en 3 dimensiones (utiliza un programa de diseño basado en figuras geométricas para hacer el objeto en computadora y después imprimirlo en un objeto de 3 dimensiones).
| Cubismo Picasso |
| Cubismo, Juan Gris |
| Mario bros, Nintendo 64 |
| Impresora 3D |
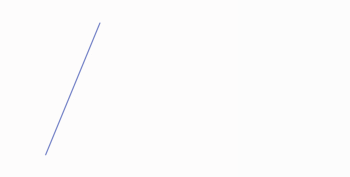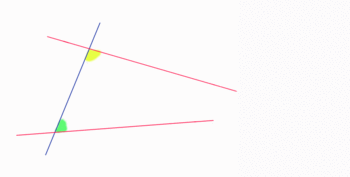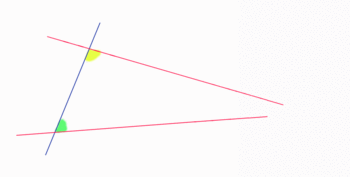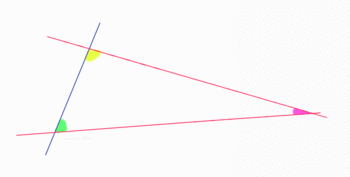
No hay comentarios:
Publicar un comentario